Avez-vous déjà raté une recette ou un projet de bricolage à cause d’une erreur de conversion ? Ce problème quotidien touche de nombreuses personnes lors de leurs activités culinaires ou techniques. Selon le Bureau International des Poids et Mesures, les erreurs d’unités causent régulièrement des dysfonctionnements. Heureusement, maîtriser un tableau de conversion transforme ces calculs complexes en manipulations simples, permettant des conversions précises sans erreurs mathématiques.
Qu’est-ce qu’un tableau de conversion et pourquoi l’utiliser ?
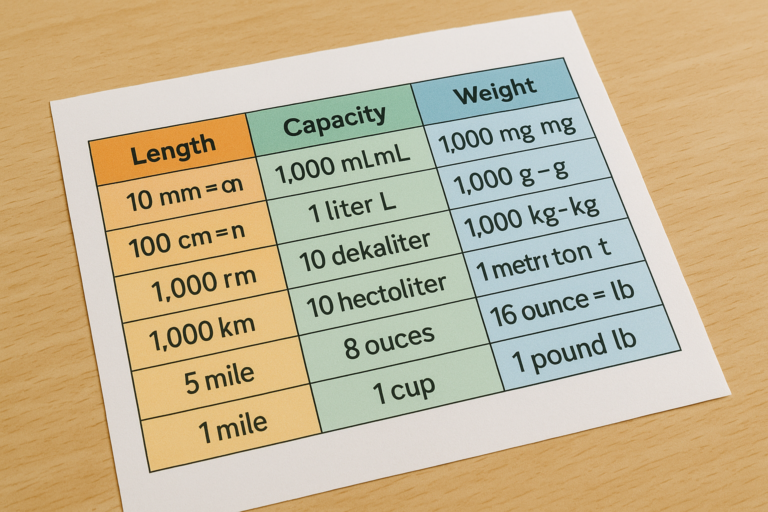
Un tableau de conversion est un outil mathématique qui permet de transformer une unité de mesure en une autre au sein d’une même grandeur physique. Il se présente sous forme de colonnes représentant les différentes unités selon le système international d’unités (SI), utilisé officiellement dans 95% des pays du monde.
Ce système facilite les calculs en évitant les erreurs de multiplication ou division. Vous placez simplement votre nombre dans la bonne colonne et lisez le résultat dans l’unité souhaitée.
Les domaines d’application sont nombreux : cuisine, bricolage, construction, sciences et vie quotidienne. Chaque profession utilise des unités spécifiques nécessitant des conversions précises selon les normes internationales en vigueur.
Important : Bien que pratique, le tableau de conversion présente une limite pédagogique : il ne permet pas de comprendre les relations fondamentales entre les unités. Il est préférable de comprendre que 100 cL = 1 L plutôt que de simplement déplacer des chiffres dans un tableau.
Comment construire et utiliser correctement un tableau de conversion
Chaque tableau de conversion suit une logique décimale pour les grandeurs linéaires (longueur). Les unités principales se placent au centre, avec les multiples à gauche et les sous-multiples à droite.
| km | hm | dam | m | dm | cm | mm |
| 1 | 5 | 0 | 0 |
Cette disposition respecte les puissances de 10, facilitant les déplacements de virgule pour les conversions de longueur uniquement.
Méthode d’utilisation en 4 étapes
- Identifiez l’unité de départ: placez votre nombre dans la colonne correspondante
- Repérez l’unité d’arrivée: localisez la colonne cible
- Complétez avec des zéros: remplissez toutes les cases entre les deux unités
- Lisez le résultat: le nombre formé donne votre conversion
Pour convertir 1,5 m en mm : placez 1 dans la colonne m, 5 dans dm, puis complétez avec des zéros jusqu’à mm. Résultat : 1500 mm.
Les différents types de tableaux de conversion par grandeur
Le tableau de conversion des longueurs utilise le mètre comme unité de référence du système international. Les multiples incluent :
- Kilomètre (km) : 1000 mètres
- Hectomètre (hm) : 100 mètres
- Décamètre (dam) : 10 mètres
Les sous-multiples comprennent le décimètre, centimètre et millimètre, avec un facteur de conversion de 10 entre chaque unité.
Masses (et non “poids”)
Distinction importante : La masse (en kg) est une quantité de matière, tandis que le poids est une force (en newtons, N) qui dépend de la gravité. Selon le Bureau International des Poids et Mesures, ces termes ne doivent pas être confondus.
- Tonne (t) : 1000 kg (seul multiple officiel du kilogramme dans le SI)
- Kilogramme (kg) : unité de référence du système international
- Gramme (g) : 0,001 kg
- Milligramme (mg) : 0,000001 kg
Note : Certaines unités comme le quintal (100 kg) sont utilisées dans certains secteurs mais n’appartiennent pas au système international d’unités officiel.
Volumes et capacités
Distinction cruciale : L’unité SI des volumes est le mètre cube (m³), tandis que le litre (L) est une unité de capacité équivalente à 1 dm³ (0,001 m³). Le litre n’est pas une unité SI mais est accepté pour utilisation avec le SI.
| hl | dal | l | dl | cl | ml |
| 2 | 5 | 0 | 0 |
Aires et volumes : facteurs de conversion spéciaux
Attention : Les aires et volumes ne suivent pas les mêmes règles que les longueurs :
- Pour les aires : facteur 100 entre les unités (1 m² = 100 dm² = 10 000 cm²)
- Pour les volumes : facteur 1000 entre les unités (1 m³ = 1000 dm³ = 1 000 000 cm³)
Ces tableaux nécessitent une structure différente avec plusieurs colonnes par unité pour gérer ces facteurs.
Exemples pratiques de conversion avec tableau de conversion
Conversions de longueurs courantes
- 3,2 km en mètres : 3200 m
- 450 cm en mètres : 4,5 m
- 15 mm en centimètres : 1,5 cm
Applications en cuisine
Pour adapter une recette de 4 à 8 personnes, vous doublez les quantités. Si la recette demande 25 cl de lait, vous aurez besoin de 50 cl soit 0,5 litre.
Le tableau de conversion des capacités simplifie ces calculs sans calculatrice.
Situations de bricolage
Lors d’achats de matériaux, les fournisseurs utilisent différentes unités. Les planches se vendent au mètre, mais les vis au millimètre. Les surfaces s’expriment en m², nécessitant la compréhension des facteurs de conversion spécifiques aux aires.
Erreurs fréquentes et astuces pour les éviter
L’erreur principale consiste à mal positionner le chiffre de départ. Chaque chiffre doit occuper une seule case du tableau.
Pour 2,35 m : placez 2 dans la colonne m, 3 dans dm et 5 dans cm. Ne regroupez jamais plusieurs chiffres dans une même colonne.
Confusion entre unités similaires
Les débutants confondent souvent décimètre (dm) et décamètre (dam). Retenez que les préfixes “déci” indiquent une division par 10, tandis que “déca” signifie une multiplication par 10.
Mémorisation des préfixes du système international
| Préfixe | Symbole | Facteur |
| méga | M | ×1 000 000 |
| kilo | k | ×1000 |
| hecto | h | ×100 |
| déca | da | ×10 |
| déci | d | ÷10 |
| centi | c | ÷100 |
| milli | m | ÷1000 |
| micro | μ | ÷1 000 000 |
Note : Depuis novembre 2022, le SI compte 24 préfixes officiels, dont les plus récents (ronna, quetta, ronto, quecto) sont utilisés pour les très grands et très petits nombres en astrophysique et en physique quantique.
Alternatives au tableau de conversion traditionnel
Méthode des bonds
Cette technique consiste à multiplier ou diviser par 10 autant de fois que nécessaire pour les longueurs. Pour passer de m à mm, vous effectuez 3 bonds vers la droite, soit 3 multiplications par 10.
Attention : Cette méthode ne s’applique qu’aux longueurs, masses et capacités, pas aux aires et volumes.
Règles de conversion directe
Certains professionnels mémorisent les facteurs de conversion :
- 1 km = 1000 m
- 1 m = 100 cm
- 1 litre = 1000 ml
- 1 m² = 100 dm² (facteur 100 pour les aires)
- 1 m³ = 1000 dm³ (facteur 1000 pour les volumes)
Cette approche convient aux conversions répétitives mais demande plus de mémorisation que le tableau de conversion, tout en favorisant une meilleure compréhension conceptuelle des rapports entre unités.
FAQ
Peut-on utiliser un tableau de conversion pour les unités de temps et comment procéder ?
Oui, mais avec des précautions importantes. Contrairement aux unités décimales, les unités de temps ne suivent pas le système décimal : 1 heure = 60 minutes = 3600 secondes. Un tableau de conversion temporel nécessite donc des colonnes spéciales avec des facteurs 60 et non 10. Pour convertir, vous devez multiplier ou diviser par 60 pour passer d’une unité à l’autre (heures ↔ minutes ↔ secondes), ce qui rend la méthode traditionnelle moins pratique que pour les unités SI classiques.
Comment adapter un tableau de conversion pour les unités anglo-saxonnes (pouces, pieds, yards) ?
Les unités anglo-saxonnes nécessitent un tableau spécialisé car elles ne suivent pas le système décimal. Les facteurs de conversion sont : 1 pied = 12 pouces, 1 yard = 3 pieds = 36 pouces, 1 mile = 1760 yards. Vous devez créer un tableau avec ces facteurs spécifiques et multiplier/diviser selon ces rapports. Pour convertir vers le système métrique, retenez que 1 pouce = 2,54 cm exactement, cette conversion servant de référence officielle entre les deux systèmes.
Existe-t-il des tableaux de conversion pour les unités de pression et de force ?
Oui, bien que plus complexes. Pour la pression, l’unité SI est le pascal (Pa), avec des multiples comme le kilopascal (kPa) et le mégapascal (MPa) suivant le système décimal. Cependant, d’autres unités coexistent : bar (1 bar = 100 000 Pa), atmosphère (1 atm = 101 325 Pa), mmHg. Pour la force, l’unité SI est le newton (N) avec ses multiples décimaux, mais on trouve aussi le kilogramme-force (1 kgf ≈ 9,81 N). Ces conversions nécessitent des tableaux spécialisés avec facteurs non-décimaux.
Comment gérer les conversions d’unités composées comme la vitesse ou la densité avec un tableau ?
Les unités composées (km/h, g/cm³, m/s²) nécessitent de convertir séparément chaque composant. Pour convertir 72 km/h en m/s : convertissez d’abord 72 km en 72 000 m, puis 1 h en 3600 s, enfin calculez 72 000 ÷ 3600 = 20 m/s. Un tableau de conversion simple ne suffit pas ; il faut décomposer l’unité, convertir chaque partie individuellement, puis recombiner. Cette méthode s’applique à toutes les unités dérivées du SI.
Quelles sont les règles de précision et d’arrondis lors de l’utilisation d’un tableau de conversion ?
La précision du résultat ne peut jamais dépasser celle de la mesure initiale. Si vous partez de 2,5 m (2 chiffres significatifs), le résultat en mm sera 2500 mm, pas 2500,0 mm. Pour les calculs scientifiques, conservez un chiffre supplémentaire pendant les étapes intermédiaires et arrondissez seulement au résultat final. En contexte professionnel, respectez les tolérances du domaine : ±1 mm en menuiserie, ±0,1 g en pharmacie. Les erreurs d’arrondi peuvent s’accumuler lors de conversions multiples successives.